
If your function is one-to-one, you can draw its inverse by clicking Invert.

The horizontal line test is performed, and the title indicates whether the function you've drawn passes this test (so it is one-to-one). Since the domain of the inverse is the range of f x and the range of the inverse is the domain of f x, this means that in order for f x to be invertible, its graph must satisfy the horizontal line test : Each horizontal line through the graph of y = f x must intersect that graph exactly once.Ĭlick and drag with your mouse to draw a function in the plot below.
This is because for the inverse to be a function, it must satisfy the property that for every input value in its domain there must be exactly one output value in its range the inverse must satisfy the vertical line test. In order for the function f x to be invertible, the problem of solving x = f y for y must have a unique solution. Ī function f x is one-to-one if distinct input values are mapped by f x to distinct output values. The \ average \ of \ happy \ and \ sad \ is \ neutral.A function f x is invertible if for every point y in the range of f x the equation y = f x can be uniquely solved for x. That is why they are spaced apart, not to make them "spacey." \(\displaystyle \ of \ the \ lower \ summation \ is \ "n" \ below \ it \ ?\) \(\displaystyle The \ lower \ limit \ of \ the \ upper \ summation \ is \ "x = 2" \ and \ the \ upper\ limit\) To reasonably explain it, *someone* would have submitted it without previewing it first. Then they are too close together and it has to be fixed. Such functions are referred to as injective. In a one-to-one function, given any y there is only one x that can be paired with the given y.
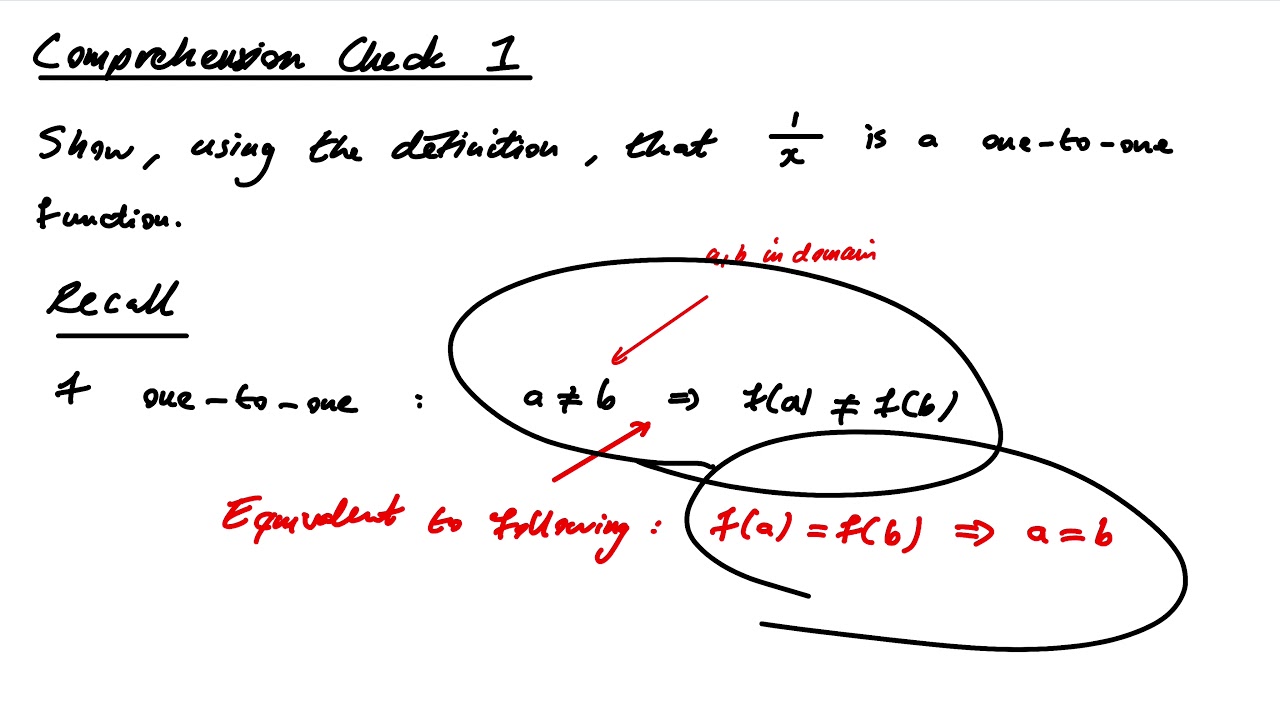
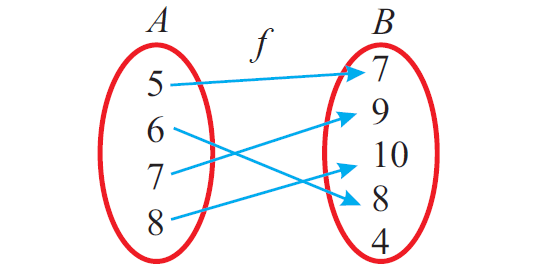
No element of B is the image of more than one element in A. Is this function onto If it is onto, for every natural number ,say y, we should search another natural number x such that f ( x) y. A function f from A to B is called one-to-one (or 1-1) if whenever f (a) f (b) then a b. When they are crammed so that they are meshed together, Apply the definition of a one-one function that is: f ( x) f ( y) x y. Seriously, it didn't look "fine" at all it was a mess/mesh of symbols. Your being able to tell is irrelevant as the readers are the ones who need to tell what they are.


 0 kommentar(er)
0 kommentar(er)
